Statistical Analysis
The Archeological Problem
Our knowledge of ancient buildings depends on understanding the principles used in their design and construction. At the core of these principles lies a system of communication through units of linear measurement, i.e., quantum units, used by architects to proportion and order the buildings, and by masons to construct them. Ancient Greek buildings were constructed from carefully hewn blocks of marble or fine limestone, each cut to the millimeter to fit a specific position within each course of the structure. Scholars agree that the design, proportion, and construction of ancient Greek buildings have their bases in quantum units. The nature and dimension of those quanta, however, are among the most bitterly contested aspects of Greek architectural history. While the quanta used by ancient Greeks architects have been intensely debated since the 1830s, the question had not been treated statistically until the recent work of Pakkanen, who applied Kendall’s (1974) cosine quantogram to estimate the possible quantum units used in isolated examples of ancient Greek structures (Pakkanen, 2004a, 2004b, 2005).
Tantalized by the instructions of the ancient architect Vitruvius, by ancient metric reliefs illustrating “official” lengths of feet, by inscriptions specifying the size of blocks and buildings, and by ancient measuring devices, Greek archaeologists since the 19th century have sought a method for assessing the units of measure used in the design of ancient Greek architecture. Given the ordered nature of Greek architecture, the unit of measure is a key for understanding the structure of a particular building, reconstructing its missing elements, establishing regional and chronological relationships between buildings, and grasping the dynamics of the design process more generally. From the ancient sources we know that architects could design according to a foot-unit, a set of proportional relationships, or a standard module. Determining which technique served as the design basis for a particular building is complicated by a number of factors, including: the possibility that a combination of techniques was used; the potential difference between the designed and the as-built dimensions; the fragmentary state of the evidence; and the varying lengths associated with the ancient foot-unit. Scholars are deeply divided on the nature of the ancient quantum unit. Some, such as Wilson Jones (2000) hold that only a few standard quantum units were used while others, such as de Waele (1995, 1997) are committed to the idea that a discrete foot-unit was established for each building. Figure 1 (taken from Rottländer (1996) illustrates a variety of proposed units of linear measure used in the ancient world.
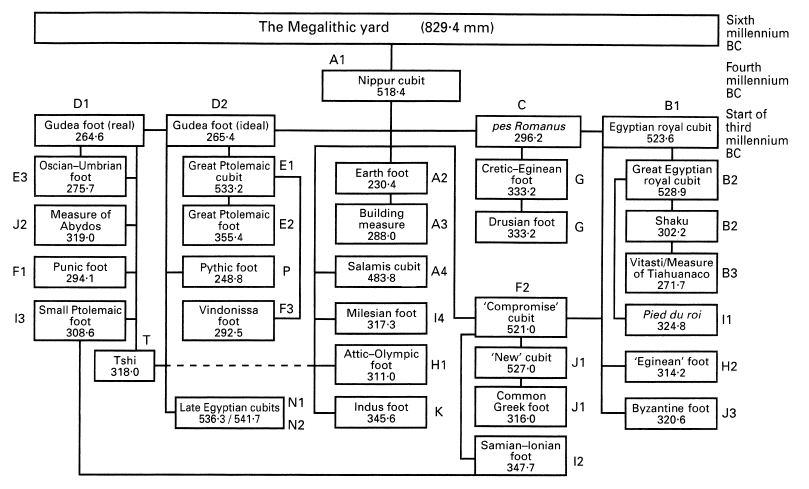
Figure 1. Proposed units of linear measure used in the ancient world (taken from Rottländer [1996]).
Although evidence of measurement standards and systems is abundant for the highly centralized ancient Egyptian and Roman societies, such documentation is scarce and conflicted in the decentralized world of ancient Greece. Unfortunately, they had no National Bureau of Standards. There is evidence to suggest a certain amount of standardization at the local and regional level. Reliefs such as the Ashmolean relief and the Salamis relief shown in Figures 2a and 2b below were set in the agora (civic center) and thus served as a common standard for local quanta.

Figure 2(b) (right) The Salamis Relief, circa 4th century BCE. From the Piraeus Museum, Piraeus, Greece.
The extensive architectural remains in the Sanctuary of the Great Gods on Samothrace provide one of the most innovative and best-preserved records of Hellenistic architecture in the eastern Mediterranean. Almost every building holds a special place in the history of Greek architecture: the Rotunda of Arsinoë is the largest round building in the ancient Greek world; the Stoa is the longest in the northern Aegean; the Propylon of Ptolemy II is uniquely bilingual, with its Ionic east façade and Corinthian western façade; the Hieron stands alone in Greek architecture for its internal apse; the Hall of Choral Dancers has one of the most complex roof structures ever attempted. The innovations we witness, however, emerge within the context of standard building practices that relied on ordering conventional shipments of marble from the mainland quarries, building according to well established techniques of construction, and drawing on a standard array of design choices. Collectively, the buildings offer an ideal opportunity to investigate questions about the quanta used in their design and construction.
Lacking its own marble quarries, architects working on Samothrace had to order material from marble quarries. We have identified marble from the disparate quarries at Thasos, Paros, Penteli, and Proconnesos; in several buildings the different marbles are deftly combined. Clear communication of the material order required a recognizable system of communication for the required sizes of blocks, i.e. a quantum. Ancient inscriptions from other sites specify the dimensions of material in terms of quanta based on a foot unit. A key question, however, is which foot unit. Several major and a dozens of lesser-used units have been identified. Thus far, no systematic attempt has been made to identify any quantum unit(s) used on Samothrace.
The questions we aim to address include the following. Were the buildings designed according to a modular unit or a foot unit? If masons followed their marble from quarry to construction, should we be able to find a connection with the ancient Thasian “foot unit” (as identified by French archaeologists)? How do we understand the metric/construction process when two buildings of very close design (the Hieron and Altar Court) are constructed of blocks marginally different in size? How can we determine if these highly diverse, expensive buildings constructed in the Sanctuary within a very short period of time and mostly of the same imported marble share commonalities of quanta? How can a deeper understanding of module, proportion, and measure lead us closer on the one hand to the practicalities of Greek construction, and on the other to their sophisticated perceptual play on our senses? Can identifying the quanta lead to a sharper sense of the architect? Can identifying the quantum units provide more definitive evidence for associating buildings within the Sanctuary to those in other major Hellenistic centers? There are, for example, close stylistic connections between the Propylon of Ptolemy II and the North Propylon in the Sanctuary of Asklepios at Epidauros, or between the Dedication of Philip III and Alexander IV and the Choregic Monument of Nikias in Athens. Understanding the quantum units used in these buildings would go to the core of our understanding of their relationship, especially the question of whether they might share a designing architect, because it would allow us to track and compare both the design and construction process.
From these estimated quanta, and more particularly the statistical methods developed to derive them, we can construct further hypotheses concerning the buildings, masons, and architects across the Mediterranean. Thus, to generalize to other ancient Greek sites and to other civilizations, comparison of quantum estimates between different buildings and sites may help to establish relationships between communities and further enhance our understanding of migration patterns.
The Statistical Problem
Data are said to have a quantum unit, or to be “quantal” or to have “quantality”, when there is an underlying periodicity in the data or a hidden unit fundamental to the process that gives rise to the data. Quantal data typically exhibit regularly spaced modes. Although we are describing an application in archaeology, and, indeed, many of the applications have been in this field, there have been applications elsewhere, such as in physics, cosmology, and biology. Çankaya and Fieller (2009) give a thorough description of several applications as well as the most recently described statistical properties for the relevant methodology. However, they do not describe a method for comparing quantal units.
The analysis of quantality has its roots in the early part of the 20th century when von Mises (1918) developed a statistical theory for estimation of quanta with application to the estimation of atomic weights, and, in particular, to show that these were limited to the positive integers. Broadbent (1955) solved this problem de novo in the 1950s with respect to the existence and estimation of the megalithic yard in British stone circles. Kendall (1974) revisited Broadbent’s work and proposed the cosine quantogram as a method for estimation.
Over the last decade, Pakkanen, a Finnish archaeologist at the University of London, has used the cosine quantogram to estimate the quanta used in buildings at several archaeological sites in Greece. For the Toumba building at Lefkandi, an early Iron Age site, Pakkanen estimates that a design unit of 0.4895 m was used (2004a). For the Temple of Zeus at Stratos, one of the most significant Early Hellenistic buildings in mainland Greece, he estimates that a design unit of 0.1053 m was used (2004b). For the Temple of Athena Alea at Tegea, he estimates that a design unit of 0.099 m was used (2005). Significantly, none of these approximates an ancient Greek foot-unit. Instead they suggest a design module. Results such as these need verification to be convincing to the archeological audience.

